Перенос, масштабирование и вращение

Масштабирование

При работе с растровой графикой очень частая операция — масштабирование объектов. Суть операции в том, чтобы число X₀ в диапазоне от A₀ до B₀ превратить в число X₁ в диапазоне от A₁ до B₁ с соблюдением пропорций:

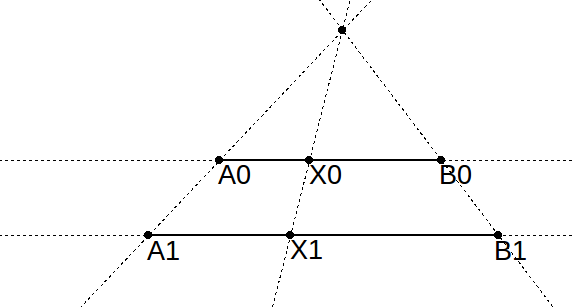
Значение X₀ сначала надо нормализовать: перевести из диапазона A₀…B₀ в диапазон 0…1. Для чего из X₀ надо вычесть нижнюю границу диапазона A₀ и поделить результат на длину диапазона B₀-A₀: X=(X0-A0)/(B0-A0)

Затем перевести в новый диапазон A₁…B₁ теми же операциями в обратном порядке. Получаем функцию переноса с масштабированием scale():

   1 def scale(A0,B0,A1,B1,x):
   2   return float(X0-A0)/(B0-A0)*(B1-A1)+A1

Проверим, как это выглядит с помощью Черепашки:

   1 def AxB(A,B,x,y):
   2   up()
   3   goto(A,y)
   4   down()
   5   stamp()
   6   goto(x,y)
   7   stamp()
   8   goto(B,y)
   9   stamp()
  10   up()
  11 
  12 A0,B0,X0 = -50,120,81
  13 AxB(A0,B0,X0,40)
  14 # Теперь масштабируем X0
  15 A1,B1 = -100,200
  16 X1 = scale(A0,B0,A1,B1,X0)
  17 AxB(A1,B1,X1,-40)

Поворот

Более подробно см Поворот в Википедии.

Вспомним¸ что sin угла и cos угла — это длины противолежащего и прилежащего катетов в прямоугольном треугольнике с единичной гипотенузой:

Обратим внимание, что картинка также иллюстрирует поворот на угол A против часовой стрелки точки пересечения положительной полуоси абсцисс и единичной окружности с центром в начале координат.

Сравнительно несложно (поворотом этой картинки на произвольный угол) доказать, что поворот любой точки на единичной окружности аналогичен, и получить следующую функцию поворота точки M на угол A относительно точки (0,0):

   1 def rotate(M,A):
   2   X=M[0]*cos(A)-M[1]*sin(A)
   3   Y=M[1]*cos(A)+M[0]*sin(A)
   4   return X,Y

Проверим:

TODO