Перенос, масштабирование и вращение

Примеры в этом тексте используют объекты из модулей math и turtle:

   1 from math import *
   2 from turtle import *

Масштабирование

При работе с растровой графикой очень частая операция — масштабирование объектов. Суть операции в том, чтобы число X₀ в диапазоне от A₀ до B₀ превратить в число X₁ в диапазоне от A₁ до B₁ с соблюдением пропорций:

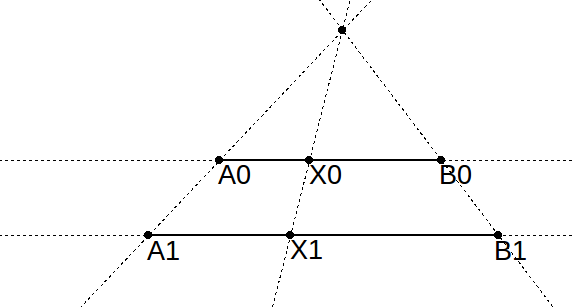
Значение X₀ сначала надо нормализовать: перевести из диапазона A₀…B₀ в диапазон 0…1. Для чего из X₀ надо вычесть нижнюю границу диапазона A₀ и поделить результат на длину диапазона B₀-A₀: X=(X0-A0)/(B0-A0)

Затем перевести в новый диапазон A₁…B₁ теми же операциями в обратном порядке. Получаем функцию переноса с масштабированием scale():

   1 def scale(A0,B0,A1,B1,x):
   2     return float(x-A0)/(B0-A0)*(B1-A1)+A1

Проверим, как это выглядит с помощью Черепашки:

   1 def AxB(A,B,x,y):
   2     up()
   3     goto(A,y)
   4     down()
   5     stamp()
   6     goto(x,y)
   7     stamp()
   8     goto(B,y)
   9     stamp()
  10     up()
  11 
  12 A0,B0,X0 = -50,120,81
  13 AxB(A0,B0,X0,40)
  14 # Теперь масштабируем X0
  15 A1,B1 = -100,200
  16 X1 = scale(A0,B0,A1,B1,X0)
  17 AxB(A1,B1,X1,-40)

Поворот

Более подробно см Поворот в Википедии.

Вспомним¸ что sin угла и cos угла — это длины противолежащего и прилежащего катетов в прямоугольном треугольнике с единичной гипотенузой:

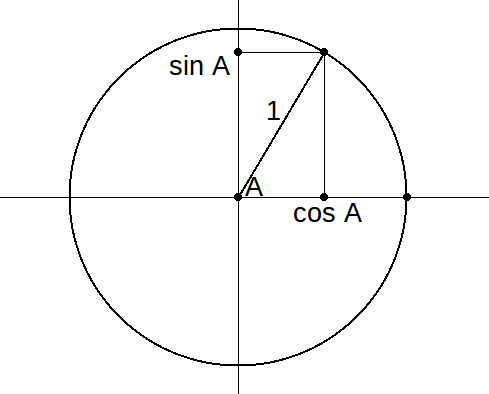
Обратим внимание, что картинка также иллюстрирует поворот на угол A против часовой стрелки точки пересечения положительной полуоси абсцисс и единичной окружности с центром в начале координат.

Сравнительно несложно (поворотом этой картинки на произвольный угол) показать, что поворот любой точки на единичной окружности аналогичен, и получить следующую функцию поворота точки M на угол A относительно точки O:

   1 def rotate(M,O,A):
   2     X=(M[0]-O[0])*cos(A)-(M[1]-O[1])*sin(A)+O[0]
   3     Y=(M[1]-O[1])*cos(A)+(M[0]-O[0])*sin(A)+O[1]
   4     return X,Y

Проверим. Зададим функцию рисования ломаной по точкам:

   1 def draw(line,col="black"):
   2     up()
   3     goto(*line[0])
   4     down()
   5     color(col)
   6     for x,y in line[1:]:
   7         goto(x,y)
   8     up()

Убедимся, что поворот на угол, близкий к pi относительно (0,0) переносит фигуру из первого в третий квадрант (при повороте ровно на pi будет наблюдаться центральная симметрия):

   1 l = [(100,200),(200,50),(50,100),(150,50)]
   2 ll = [rotate(m,(0,0),2.75) for m in l]
   3 draw(l)
   4 draw(ll)

Перенос + масштабирование + поворот ломаной

Осталось решить, какая точка в операции «перенос + масштабирование + поворот ломаной» будет служить началом координат. Несложно написать функцию масштабирования+переноса фигуры, вписанной в прямоугольник с левым нижним углом в точке m₀ и правым верхним углом в точке M₀, которая порождает подобную фигуру, вписанную в прямоугольник m₁:M₁. Однако после поворота (неважно вокруг чего) описанный прямоугольник, скорее всего, окажется другим. Логично за центр поворота взять центр результирующего прямоугольника, хотя в этом случае после поворота фигура может не вписаться в него.

Получаем функцию переноса+масштабирования ломаной (списка точек) в прямоугольнику m:M и последующего поворота его на угол alpha:

   1 def rotoscale(dots,m,M,alpha):
   2     # списки абсцисс и ординат
   3     X,Y = zip(*dots)
   4     mx,Mx,my,My=min(X),max(X),min(Y),max(Y)
   5     # перенос+масштабирование всех точек
   6     ds = [(scale(mx,Mx,m[0],M[0],x),scale(my,My,m[1],M[1],y)) for x,y in dots]
   7     center = (m[0]+M[0])/2.,(m[1]+M[1])/2.
   8     # поворот всех точек относительно центра целевого прямоугольника
   9     return [rotate(d,center,alpha) for d in ds]

Посмотрим, как работает эта функция:

   1 reset()
   2 # исходный многоугольник
   3 l = [(-50,50),(30,40),(50,-30),(-30,-50),(-50,50)]
   4 draw(l,"blue")
   5 # позиция повёрнутого + масштабированного прямоугольника, размер описанного квадрата
   6 pos, w = (100,100), 50
   7 # количество копий
   8 N = 6
   9 for i in xrange(N):
  10     a = pi*2*i/N
  11     # где размещать очередную копию
  12     p = rotate(pos, (0,0), a)
  13     # в какой квадрат вписывать
  14     diag = ((p[0]-w/2,p[1]-w/2), (p[0]+w/2, p[1]+w/2))
  15     ll = rotoscale(l, diag[0], diag[1], a)
  16     draw(ll,"red")
  17     # увеличим размер
  18     w+=15

Другой вариант — функция, которая выдаёт фигуру, строго вписывающуюся в m:M уже после поворота. Правда, в этом случае трудно соблюсти исходные пропорции.