Моделирование структур данных
На примере работы со стеком и кадром хорошо виден главный недостаток программирования в машинных кодах и на языке Ассемблера — отсутствие готовых моделей для популярных абстрактных данных, таких как структуры, связные списки, деревья и т. д. Попытка внедрить такие модели в синтаксис языка ассемблера неминуемо нарушит его главное свойство: «прозрачность» трансляции инструкций в машинные команды.
Однако заниматься моделированием структур данных время от времени приходится. Эта тема не прибавит новых фактов к нашему знанию об архитектуре ЭВМ, зато мы составим представление о том, как абстрактные типы данных могут быть организованы на уровне машинных кодов и линейно адресуемой памяти. Кроме того, необходимо попрактиковаться в написании различных простых алгоритмов перед тем, как мы возьмёмся рассматривать более сложные аппаратные механизмы, в которых эти алгоритмы, возможно, придётся использовать.
Нас будут интересовать два вопроса:
- Нет ли в реализации относительно простых типов данных каких-нибудь особенностей, которые накладывает архитектура? (особенности есть)
- Насколько трудоёмко делать на языке ассемблера алгоритмическую поддержку более сложных типов данных? (ожидаемо сложно, но выполнимо)
Массивы
Разговаривая о косвенной адресации, мы уже рассматривали массивы простых типов (машинных слов, полуслов и байтов).
Все данные одного размера (более того — одного типа)
- В языке ассемблера нет возможности отличить целое число от вещественного одинарной точности: они имеют одинаковый размер
- Все данные размещены в памяти непрерывно
Количество данных строго ограничено т. н. верхним индексом массива — номером последнего элемента, после которого, возможно, находятся другие данные
⇒ операция индексирования (нахождения элемента по номеру) в массиве очень эффективна:
Адрес_элемента_k = Адрес_начала_массива + k * размер_одного_элемента
(манипуляция с индексами и размером элемента носит название адресной арифметики)
Массивы можно представлять многомерными, но реализуются они всё равно как непрерывный фрагмент памяти. От одномерного массива многомерный отличается только способом индексации.
Двумерный массив (матрица)
- Имеет две координаты — абсциссу x и ординату y
Характеризуется двумя верхними индексами — шириной M и высотой N матрицы
- Содержит M*N элементов
Адрес Axy элемента массива A с координатами x,y:
Axy=A+(x+y*M)*b, где b — размер элемента в байтах
такой массив располагается в памяти построчно (сначала нулевая строка матрицы, потом первая и т. д.)
Для многомерного массива:
Каждый элемент характеризуется группой индексов (координатами) фиксированной для данного массива размерностью d
По каждой из координат зафиксирован наибольший индекс W0, W1, …, Wd-1
Адрес элемента массива AX0X1…Xd-1^ = A+(X0+(X1+(X2+…+(Xd-1)*Wd-2)…)*W1)*W0))*b
Операция поиска элемента в массиве размера N требует в среднем N/2 сравнений, если елемент в массиве еть, и ровно N сравнений, если его там нет:
1 .data
2 arrayN: .word 10 # Длина массива
3 array: .word 1 3 5 7 9 11 13 15 17 19 21
4
5 .text
6 la a0 array
7 lw a1 arrayN
8 li a2 13 # Искомый элемент
9 call afind # Вызов подпрограммы
10 li a7 1
11 ecall
12 li a7 10
13 ecall
14
15 # Поиск value в массиве array длиной width
16 # Возвращается индекс, если элемент найден, иначе — -1
17 afind: # array width value → position
18 li t1 0 # Инициализация: Индекс
19 anext: lw t0 (a0) # Очередной элемент массива
20 beq t0 a2 adone # Искомый элемент найден
21 addi a0 a0 4 # Изменение: адрес элемента
22 addi t1 t1 1 # Изменение: индекс
23 blt t1 a1 anext # Проверка условия: индекс меньше длины
24 li t1 -1 # Элемент не найден, надо вернуть -1
25 adone: mv a0 t1
26 ret
В этом примере массив имеет длину 10, а в директиве .word — 11 элементов. Значит, последнее число в ней (21) не принадлежит массиву и не должно быть найдено (
 проверьте!)
проверьте!)
Стек
Свой собственный стек (LIFO, Last In — First Out) можно реализовать с помощью массива практически так же, как организован стек для подпрограмм. Если заданный вручную стек будет расти вверх, а не вниз, как системный, к его элементам можно будет обращаться как к элементам обычного массива. Всё, что потребуется дополнительно — это знание о том, сколько элементов находится в нём в данный момент, например, в виде адреса вершины стека (первой незанятой ячейки в нём).
Как и в массиве, операция поиска по стеку, в котором находится N элементов, требует в среднем N/2 сравнений, если искомый элемент в нём есть, и ровно N — если его там нет
- Добавление элемента на вершину собственного стека и снятие элемента оттуда так же эффективны, как и в случае системного: достаточно однократно записать / прочитать значение и изменить адрес вершины
Работая со стеком как с хранилищем данных, мы можем захотеть, чтобы указатель на вершину хранился в отдельном регистре, хотя бы временно — тогда его эффективность станет идентична эффективности системного. Платой за это будет запрет на использование этого регистра где бы то ни было ещё.
Стек также можно использовать и как обычный массив, разделяя его ячейки на «занятые» (от корня стека до его вершины) и «свободные» (от вершины до выделенной границы).
Появляется возможность записывать значение не только на вершину стека, но и вообще в произвольное место. Правда, в отличие от работы с вершиной, такая операция будет требовать перестановки сразу нескольких элементов массива (в среднем — половины). В самом деле, чтобы вставить некоторой значение на позицию K в массив из N элементов, необходимо сделать так, чтобы K-я ячейка массива была не занята — «сдвинуть» часть элементов массива:
- Увеличить N до N+1
- Переставить N-й элемент на N+1-е место
- Переставить N-1-й элемент на N-е место
- …
- Переставить K+1-й элемент на K+2-е место
- Переставить K-й элемент на K+1-е место
Только после этого можно на освободившееся K-е место вписывать новое значение.
 В алгоритме выше мы начинаем сдвиг с конца массива. А можно ли было начать с K-го элемента и сдвигать до конца?
В алгоритме выше мы начинаем сдвиг с конца массива. А можно ли было начать с K-го элемента и сдвигать до конца?
1 .eqv SSIZE 128 # Размер стека (не используется)
2
3 # Положить регистр %register на вершину стека %top
4 .macro push %top %register
5 addi %top %top 4
6 sw %register -4(%top)
7 .end_macro
8
9 # Снять с вершины стека %top значение в регистр
10 .macro pop %top %register
11 lw %register -4(%top)
12 addi %top %top -4
13 .end_macro
14
15 # Вставить значение %register в массив %stack перед позицией %index
16 # Массив — это стек, вершина которого указана параметром %top
17 .macro insert %top %index %stack %register
18 mv a0 %top
19 mv a1 %index
20 la a2 %stack
21 mv a3 %register
22 call insert_sub
23 mv %top a0
24 .end_macro
25
26 # Удалить элемент массива %stack в позиции %index
27 # Массив — это стек, вершина которого указана параметром %top
28 .macro delete %top %index %stack
29 mv a0 %top
30 mv a1 %index
31 la a2 %stack
32 call delete_sub
33 mv %top a0
34 .end_macro
35
36 .data
37 .align 2
38 stack: .space SSIZE
39 .text
40 la s11 stack # Указатель на вершину нашего стека
41 li t0 16
42 mloop: push s11 t0 # Положим на стек 16 чисел (16…1)
43 addi t0 t0 -1
44 bgtz t0 mloop
45 pop s11 t0 # Снимем со стека два значения
46 pop s11 t0
47 li s2 -5
48 li s1 8
49 miloop: insert s11 s1 stack s2 # Добавим 5 чисел в позиции 8 (-5…-1)
50 addi s2 s2 1
51 bltz s2 miloop
52 li s2 5
53 li s1 4
54 mdloop: delete s11 s1 stack # Удалим 5 чисел в позиции 4
55 addi s2 s2 -1
56 bgtz s2 mdloop
57 li a7 10
58 ecall
59
60 # Процедура удаления элемента в позиции index из массива stack с вершиной стека в top
61 delete_sub: # top index stack
62 slli a1 a1 2 # Превращаем индекс в смещение в байтах
63 add a1 a1 a2 # Адрес удаляемого элемента
64 mv t1 a1
65 dloop: bgeu t1 a0 ddone # Пока не добрались до вершины стека…
66 lw t0 (t1) # Копируем следующий элемент на место предыдущего
67 sw t0 -4(t1)
68 addi t1 t1 4
69 j dloop
70 ddone: addi a0 a0 -4 # Сдвигаем и возвращаем вершину стека
71 ret
72
73 # Процедура добавления элемента value перед позицией index массива stack с вершиной в top
74 insert_sub: # top index stack value
75 slli a1 a1 2
76 add a1 a1 a2 # Адрес места вставки
77 mv t1 a0 # Начало с вершины стека
78 addi a0 a0 4 # Сдвигаем вершину стека
79 iloop: bltu t1 a1 idone # Пока не добрались до места вставки
80 lw t0 -4(t1) # Копируем текущий элемент в следующий
81 sw t0 (t1)
82 addi t1 t1 -4
83 j iloop
84 idone: sw a3 (t1) # Записываем value в освободившуюся ячейку
85 ret
- Здесь мы применили приём «макрос + подпрограмма» — в тексте программы вызов соответствующей операции над массивом занимает одну строку, но макрос всего лишь подготавливает вызов подпрограммы, и обрабатывает результат.
- Можно было бы нарисовать красивую диаграмму — как переставляются значения в массиве, но лучше всего — пройти программу пошагово в RARS, наблюдая все эти перестановки в окне «Data Segment».
Переполнение, опустошение и выход за вершину стека
Приведённая выше реализация стека эффективна, однако требует довольно жёсткой дисциплины использования, так как в ней не проверяются различные варианты выхода за его границы.
Выход за границы стека — это ситуация, при которой при работе со стеком данные записываются или читаются по адресам за пределами диапазона от начала до вершины стека.
Можно различить опустошение стека — попытку снять больше данных, чем есть на нём в данный момент (например, pop из пустого стека);
переполнение — попытку положить на стек больше данных, чем помещается в области между вершиной и границей массива, который отведён на стек (например, push в заполненный стек)
выход за пределы стека при чтении из соответствующего массива с ошибочным индексом
Чаще всего сам выход за границы происходит намного позже актуальной ошибки работы со стеком, и в другом месте программы. При работе с системным стеком это настолько опасно, что был изобретён механизм кадра.
Для того, чтобы ваш код не испортил стек, соблюдайте правило:
Кто и сколько на стек кладёт, тот столько оттуда и снимает
 В качестве самостоятельного упражнения модифицируйте подпрограммы в примере выше так, чтобы исключить все три ситуации. Насколько изменится их эффективность? (нажмите «Комментарии» в шапке страницы, чтобы прочитать спойлер)
В качестве самостоятельного упражнения модифицируйте подпрограммы в примере выше так, чтобы исключить все три ситуации. Насколько изменится их эффективность? (нажмите «Комментарии» в шапке страницы, чтобы прочитать спойлер)
Структура и массив структур
- Структура
- набор разнотипных данных, размещённых подряд в оперативной памяти.
О структурах имеет смысл говорить по двум причинам.
Во-первых, структуры повсеместно используются для моделирования всевозможных составных данных. Это могут быть учётные карточки (фамилия, имя, год рождения), элементы абстрактных типов данных (узел дерева или связного списка), записи в базе данных (другое название структур — «записи»). Все наборы одной и той же структуры имеют одинаковый размер, поэтому из них удобно составлять массивы, работа с которыми отличается от работы с массивами, например, целых чисел только размером элемента.
Во-вторых, аппаратное представление структуры требует особого внимания, потому что разнотианые данные могут потребовать выравнивания, и это влияет на размер структуры.
3 машинных слова |
4 машинных слова |
3 машинных слова с упаковкой |
|
|
|
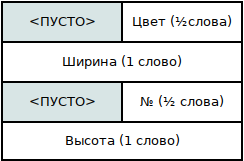
- В первом случае нам «повезло», и два полуслова «упаковались» в одно машинное слово без выравнивания. Размер струтуры оказался 12 байтов, а смещение полей «ширина», «цвет», «№» и «высота» внутри неё — 0, 4, 6 и 8 байтов соответственно (обратите внимание на порядок!)
- Во втором случае для каждого полуслова ассемблер автоматически подставил ещё полуслово заполнителя, потому что целочисленные поля нуждаются в выравнивании адреса на границу, кратную 4. Смещения полей внутри структуры — 0, 4, 8 и 12, а суммарный размер — 16 байтов.
Третий случай — нестандартный. Мы можем программно «запихать» целое число в четыре байта, начиная с адреса, не кратного 4. В нашем случае для этого число надо разбить на два полуслова и записывать их по отдельности. Так же по отдельности будет реализовано и чтение из такой структуры. Бывает изредка нужно для экономии байтов данных.
В ассемблере RARS нет возможности уведомить программиста о том, происходило ли выравнивание или нет, и какими оказались смещения, так что рассчитывать приходится только на знания. То же самое относится и к суммарному размеру структуры.
1 # Смещения в структуре card
2 .eqv card.width 0
3 .eqv card.color 4
4 .eqv card.num 6
5 .eqv card.height 8
6 .eqv card 12 # Размер всей структуры
7
8 .macro randint %min %max
9 li a0 0
10 li a1 %max
11 addi a1 a1 -%min
12 li a7 42
13 addi a0 a0 %min
14 ecall
15 .end_macro
16
17 .data
18 .align 2
19 array: .space 60 # Массив структур
20 .text
21 li t1 5
22 la t2 array
23 loop: randint 500 1000
24 sw a0 card.width(t2)
25 randint 0 255
26 sh a0 card.color(t2)
27 randint 1 300
28 sh a0 card.num(t2)
29 randint 1000 2000
30 sw a0 card.height(t2)
31 ecall
32 addi t2 t2 card
33 addi t1 t1 -1
34 bgtz t1 loop
 Пройдите эту программу пошагово и посмотрите, как заполняется оперативная память
Пройдите эту программу пошагово и посмотрите, как заполняется оперативная память
Кольцевой буфер: очередь
Классический стек с очень большой натяжкой подходит для моделирования другого абстрактного типа данных — очереди (FIFO, First In — First Out). Дело в том, что в очереди определены две операции — добавление в хвост и снятие с головы1. И если взять из очереди так же эффективно, как снять со стека, то добавить в корень стека «стоит» довольно дорого: предварительно на до сдвигать все его элементы.
Поможет простая, но остроумная идея — т. н. кольцевой буфер.
- Кольцевой буфер
Массив фиксированного размера N, в котором определены два адреса: начало буфера head и конец буфера tail.
Операция добавления в буфер — это заполнение элемента в позиции tail и перестановка tail на следующий элемент
Операция взятия из буфера — это чтение элемента в позиции head и перестановка head на следующий элемент
Если после увеличения head или tail выходит за пределы массива, он начинает указывать на его начало
Таким образом в кольцевом буфере есть «занятое» место, между head и tail, и свободное, между tail и head, причём одно из них «перваливает» через конец буфера, продолжаясь в начале:
Добавление и взятие из очереди |
Добавление с перестановкой хвоста очереди в начало |
|
|
Строго говоря, у кольцевого буфера больше эффективных операций, чем у очереди: и добавление, и взятие элементов с обоих сторон буфера требует фиксированного числа команд, и не зависит от количества элементов в нём.
Главное усложнение по сравнению с реализацией стека: если для стека в примитивном случае достаточно одного выделенного регистра, то для очереди и двух будет мало: каждая операция должна проверять, не перевалил ли индекс за границу очереди, и переставлять его в начало. Поэтому опишем структуру, состоящую из размера очереди, её головы, хвоста и массива с элементами. Макросы и подпрограммы будут получать адрес такой структуры.
1 .macro queue %size
2 .data
3 .word %size # Размер
4 .word 0 # Индекс головы
5 .word 0 # Индекс хвоста
6 .space %size # Массив элементов
7 .space %size
8 .space %size
9 .space %size
10 .end_macro
11
12 # Поставить константу %i в очередь %queue
13 .macro puti %queue %i
14 la a0 %queue
15 li a1 %i
16 call put_q
17 .end_macro
18
19 # Взять из очереди %queue значение и тут же его вывести
20 .macro getout %queue
21 la a0 %queue
22 call get_q
23 li a7 1
24 ecall
25 li a0 '\n'
26 li a7 11
27 ecall
28 .end_macro
29
30 .data
31 Q: queue 8
32 .text
33 puti Q 11
34 puti Q 12
35 puti Q 13
36 getout Q
37 puti Q 14
38 puti Q 15
39 puti Q 16
40 getout Q
41 getout Q
42 puti Q 17
43 puti Q 18
44 puti Q 19
45 getout Q
46 li a7 10
47 ecall
48
49 put_q: # queue value
50 lw t1 (a0) # размер
51 lw t2 8(a0) # хвост
52 addi t3 a0 12 # массив
53 slli t4 t2 2 # смещение в массиве
54 add t3 t3 t4 # адрес хвоста
55 sw a1 (t3)
56 addi t2 t2 1 # сдвиг хвоста
57 blt t2 t1 putn # не превысили размер
58 li t2 0 # перевалили за конец
59 putn: sw t2 8(a0) # обновили хвост
60 ret
61
62 get_q: # queue
63 lw t1 (a0) # размер
64 lw t2 4(a0) # голова
65 addi t3 a0 12 # массив
66 slli t4 t2 2 # смещение в массиве
67 add t3 t3 t4 # адрес головы
68 addi t2 t2 1 # сдвиг головы
69 blt t2 t1 getn # не превысили размер
70 li t2 0 # перевалили за конец
71 getn: sw t2 4(a0) # обновили голову
72 lw a0 (t3) # Прочитаем элемент
73 ret
В ассемблере RARS нет вычислений периода компиляции — чтобы получить массив из %size четырёхбайтных элементов, просто повторим .space %size четырежды.
TODO  Чтобы более наглядно увидеть под отладчиком, как «вращается» кольцевой буфер, добавьте в процедуру get_q «затирание» взятого из очереди элемента (например, заполните только что освобождённую ячейку значением -1).
Чтобы более наглядно увидеть под отладчиком, как «вращается» кольцевой буфер, добавьте в процедуру get_q «затирание» взятого из очереди элемента (например, заполните только что освобождённую ячейку значением -1).
Понятие «кода ошибки»
При работе с очередью (в отличие от стека) ситуации переполнения и опустошения — штатные. Очередь используется, если нельзя предсказать как часто и когда именно элементы будут в неё вставать и выходить. Пользователя надо предупреждать о том, что операция закончилась неуспешно. С другой стороны, если дисциплина программирования достаточно жёсткая, в таком предупреждении необходимости нет. Следовательно, вариант «с предупреждением» должен быть совместимым по API2 с простым вариантом.
Вспомним, что согласно конвенции о передаче параметров возвращаемых значений может быть два — в регистре a0 и в регистре a1. Используем регистр a1 для передачи т. н. кода ошибки — информации о том, был ли вызов успешен (в этом случае возвращается 0) или нет (в этом случае возвращается число, соответствующее типу нештатной ситуации).
 Модифицируйте функции из примера выше так, чтобы put_q возвращало в a1 число 1 при попытке переполнить очередь (в остальных случаях — 0), а get_q возвращало в a1 число 1 при попытке взять элемент из пустой очереди (в остальных случаях — 0).
Модифицируйте функции из примера выше так, чтобы put_q возвращало в a1 число 1 при попытке переполнить очередь (в остальных случаях — 0), а get_q возвращало в a1 число 1 при попытке взять элемент из пустой очереди (в остальных случаях — 0).
 Какие ещё нештатные ситуации могут возникнуть при вызове этих функций? (нажмите «Комментарии» в шапке страницы, чтобы прочитать спойлер)
Какие ещё нештатные ситуации могут возникнуть при вызове этих функций? (нажмите «Комментарии» в шапке страницы, чтобы прочитать спойлер)