Циклы (1)

Разбор домашнего задания «Ввести 5 чисел, найти максимум»

Вариант решения:

   1 #include <stdio.h>
   2 main() {
   3   int a, max;
   4   scanf("%d", &max);
   5 
   6   scanf("%d", &a);
   7   if(a>max) max=a;
   8   scanf("%d", &a);
   9   if(a>max) max=a;
  10   scanf("%d", &a);
  11   if(a>max) max=a;
  12   scanf("%d", &a);
  13   if(a>max) max=a;
  14 
  15   printf("%d\n",max);
  16 }

В этом решении примечательно то, что строки с 6 по 13 повторяются по две.

Воспользуемся конструкцией

while(<выражение>) оператор;

где <выражение> трактуется как «нулевое» (ложь) и «ненулевое» (истина), а <оператор> — либо один оператор, либо блок в фигурных скобках. Работа оператора while:

1. Проверка выражения

   • если оно ложно, начать выполнять инструкции после оператора т. е. выйти из цикла

2. Выполнение оператора

3. Переход к п. 1.

Перепишем этот пример с использованием while:

   1 #include <stdio.h>
   2 main() {
   3   int a, max, i;
   4 
   5   scanf("%d",&max);
   6   i = 0;
   7   while(i<4) {
   8     scanf("%d", &a);
   9     if(max<a)
  10       max = a;
  11     i++;
  12   }
  13   printf("%d\n", max);
  14 }

Обратите внимание на то, что в цикле формально две части — условие и тело, — а фактически — четыре:

1. Инициализация переменных, участвующих в условии (i = 0;)

2. Проверка условия (while(i<4))

3. Тело

4. Изменение переменных, участвующих в условии (i++;)

Пропуск любой части цикла делает его бессмысленным, если только тело не совпадает с изменением, или вы и вправду хотели сделать цикл вечным.

В Си есть оператор, for, реализующий именно эту каноническую схему цикла:

for(<выражение>; <выражение>; <выражение>) <оператор>
  иными словами
for(<инициализация>; <условие>; <изменение>) <тело>

Некоторым ограничением является то, что инициализация и изменение в for не могут быть группой операторов, это всегда одиночные выражения. Напоминаем, что операция присваивания в Си — это именно операция, и может встречаться в выражении сколько угодно раз: например, c=a=(b=123)+2; означает «присвоить 123 в b, к результату прибавить 2 и присвоить в a, результат присвоить в c».

Перепишем пример с использованием for:

   1 #include <stdio.h>
   2 main() {
   3   int a, max, i;
   4 
   5   scanf("%d",&max);
   6   for(i=0; i<4; i++) {
   7     scanf("%d", &a);
   8     if(max<a)
   9       max = a;
  10   }
  11   printf("%d\n", max);
  12 }

Стоит заметить, что порядок выполнения «канонической схемы цикла» остался прежний: инициализация → (проверка условия/выход → тело → изменение).

Пример: все степени двойки не больше 1000

   1 #include <stdio.h>
   2 main() {
   3   int p;
   4 
   5   p=1;
   6   while(p<=1000) {
   7     printf("%d ",p);
   8     p*=2;
   9   }
  10   printf("\n");
  11 }

С циклом for:

   1 #include <stdio.h>
   2 main() {
   3   int p;
   4 
   5   for(p=1; p<=1000; p*=2)
   6     printf("%d ",p);
   7 
   8   printf("\n");
   9 }

Домашнее задание

• Прочитать в учебнике пример программы с циклом while и использование цикла for

• Ввести натуральное число n.

  • Вычислить

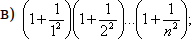
    • Замечание: деление должно быть не целочисленным, т. е. при его вычислении делимое или делитель должны быть вещественными

• Ввести натуральное число n. Поменять порядок цифр числа n на обратный.
• Ввести действительное число х.

  • Вычислить

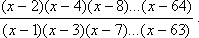
• Вычислить бесконечную сумму с заданной точностью ε (ε > 0). Считать, что требуемая точность достигнута, если вычислена сумма нескольких первых слагаемых и очередное слагаемое оказалось по модулю меньше, чем ε, - это и все последующие слагаемые можно уже не учитывать.

  • Число ε ввести в переменную eps, вычислить: ,

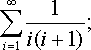    • то есть 1/(1*(1+1))+1/(2*(2+1))+1/(3*(3+1))+…

    Замечание: деление должно быть не целочисленным